Question

Jerome is writing a coordinate proof to show that the midsegment of a trapezoid is parallel to its bases. He starts by assigning coordinates as given, where RS is the midsegment of trapezoid KLMN.

Since RS is the midsegment of trapezoid KLMN, the coordinates of R are ( ____, ____ ) and the coordinates of S are (a+d,c).

The slope of KL is 0.

The slope of RS is 0.

The slope of NM is ____.

The slope of each segment is 0, therefore, the midsegment is parallel to the bases.



Answer Choices :

a, b, c, d

a+b, a+d

0, 1, 2

Answer 1

the coordinates of R are (b,c)

the coordinates of S are (a+d,c)

the slopes of all the segments is 0

Answer 2

coordinates of R(b,c)

slope of NM is 0.

Explanation:

The midpoint of the line joining the points (x₁,y₁) and (x₂,y₂) is given by

`((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2))`

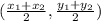
The midpoint of the line segment NK is given by

`((0+2b)/(2),(0+2c)/(2))`

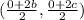
∴R(b,c)

The slope of the line joining the points (x₁,y₁) and (x₂,y₂) is given by

`m =(y_(2)-y_(1))/(x_(2)-x_(1))`

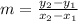
Slope of RS is

`m_(RS) =(c-c)/(a+d-b) = 0`

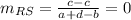
Hence

coordinates of R(b,c)

and slope of NM is 0.