Question

Violin string are parallel. Viewed from above a violin bow in two different position forms to transversal to the violin string. Usually in the provided information find The following

Answer 1

1.) You are correct.

2.) If ∠KQO = 58° and ∠AMI corresponds to it, then this means
`4x - 13y = 58`.

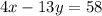Substitute for x. ⇒
`4(31) - 13y = 58`

-->
`124 - 13y = 58`

-->
`-13y = 58 - 124 --> -13y = -66`

-->
`y = (66)/(13)`

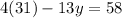
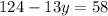
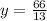
Checking your work:
`4(31) - 13((66)/(13)) = 124 - 66 = 58`

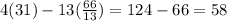
3.) To solve this problem, try to think of triangle ΔQPK. All triangle angles have a sum of 180°. We already have 58. ∠HKQ is an exterior angle with a measure of 113°, so ∠PKQ is supplementary to it. 180 - 113 is 67. Now that we have two angle measures, the sum is 125, meaning that ∠KPQ is 55°. Because ∠MPL corresponds to it, this means it has the same measure of 55°.

4.) ∠KQO and ∠QOD are alternate interior angles, since they share the same transversal. If ∠KQO = 58°, then ∠QOD is also 58°.

5.) Angle ∠MPL is supplementary to ∠LPO. 180 - 55 = 125, so ∠LPO is 125°.