Question

A bank has written a call option on one stock and a put option on another stock. For the first option the stock price is 50, the strike price is 51, the volatility is 28% per annum, and the time to maturity is nine months. For the second option the stock price is 20, the strike price is 19, the volatility is 25% per annum, and the time to maturity is one year. Neither stock pays a dividend, the risk-free rate is 6% per annum, and the correlation between stock price returns is 0.4. Calculate a 10-day 99% VaR.

Answer 1

10-Day 99% VaR = 3.61

Step-by-step explanation:

Data Given:

For First Option:

Stock Price = 50

Strike Price = 51

Volatility = 28% per annum

Time to maturity = 9 months

For Second Option:

Stock Price = 20

Strike Price = 19

Volatility = 25% per annum

Time to maturity = 12 months or 1 year

Risk Free Rate = 6% per annum

Correlation = 0.4

Find 10-day 99% VaR.

Solution:

First of all we need to refer the DerivaGem Model to dig out the change in price equation for both the options.

So, according to DerivaGem Model, We have following data:

For First Option:

Value = -5.413

Delta Value = -0.589

For Second Option:

Value = -1.014

Delta = -0.284

Change in Price = (Delta value of First Option x Stock Price)Y1 + (Delta value of the second option x Stock Price)Y2

Change in Price = (-0.589 x 50)Y1 + (-0.284 x 20)Y2

So, We will get the Change in Price Linear Equation for both the options.

Change in Price = -29.45Y1 -5.68Y2

Now, we have to calculate the Daily Volatility Percentage.

Formula:

Daily Volatility Percentage = Volatility/ Square root of number of days active in annum

Number of Days Active = 252

Volatility for First Option = 28%

Volatility for Second Option = 25%

Daily Volatility Percentage for First Option = 28%/
`√(252)`

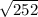
Daily Volatility Percentage for First Option = 0.0176

Similarly,

Daily Volatility Percentage for Second Option = 25%/
`√(252)`

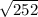
Daily Volatility Percentage for Second Option = 0.0157

Now, utilizing the above calculated data, we can find the one-day variance of change in price.

1-Day Variance =
`(29.45^(2) *0.0176^(2)) + (5.68^(2) * 0.0157^(2)) - (2 * 29.45 * 0.0176 * 5.68 * 0.0157 * 0.4)`

Solving the above equation:

We get:

1-Day Variance = 0.2396

Now, we have to find the standard deviation of 1-Day Variance:

SD of 1-Day Variance =
`√(0.2396)`

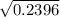
SD of 1-Day Variance = 0.4895

So,

Now, in order to find the value of one day 99% VaR from the table, we have all the prerequisites.

So,

Value of One day 99% VaR from table = 2.33

But we need 10-Day 99% VaR.

So, number of days = 10

Hence,

10-Day 99% VaR =
`0.4895 * 2.33 * √(10)`

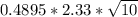
10-Day 99% VaR = 3.61