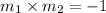Question

Lines a and b are parallel. line c is perpendicular to both line a and line B. Which statement about lines a,b and C is not true?

Answer 1

Option A) The sum of slopes of a and b is zero

Explanation:

We are given the following:

`Line ~a \parallel Line ~b`

`Line ~c \perp Line ~a\\Line ~c \perp Line ~b`

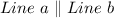
We have to find the false statement.

a) The sum of slopes of a and b is zero

The given statement is false as the parallel lines have same slope and their sum can only be zero if the slopes of both the parallel lines is zero.

b) Lines a and b have same slope

The statement is true. Parallel lines have same slope.

c) The product of slopes of line a and line c is -1

The statement is true.

As two perpendicular lines with slope
`m_1, m_2` respectively, satisfies the property:

`m_1 * m_2 = -1`

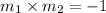
d) The product of slopes of line b and line c is -1

The statement is true.

Again, as two perpendicular lines with slope
`m_1, m_2` respectively, satisfies the property:

`m_1 * m_2 = -1`

Answer 2

When lines are parallel, they have the same slope, so the statement "line a and line b have the same slope" is TRUE

When lines are perpendicular, the slopes are opposites (the sign and number is flipped)

For example:

slope is 2

perpendicular line's slope is -1/2

slope is -1

perpendicular line's slope is 1/1 or 1

slope is 4/5

perpendicular line's slope is -5/4

When you multiply(the product) perpendicular slopes together, they equal -1. Since line c is perpendicular to line a and line b, the product of their slopes is -1.(so this is true)

The statement "the sum of the slopes of line a and b is 0" is false because if they have the same slope, when added together the result would not be 0. The slopes of line a and line b is -2/3, so the sum would be -4/3.