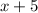Answer : The length of the base of the parallelogram is,
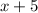
Step-by-step explanation :
As we know that:
Area of parallelogram = Height × Base
Given:
Height of parallelogram =
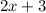
Area of parallelogram =

Now put all the given values in the above formula, we get:
Area of parallelogram = Height × Base
 =
=
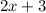 × Base
× Base
Base =
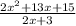
Now factorize this expression
 , we get:
, we get:
Base =
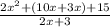
Base =
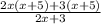
Base =
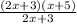
Base =
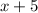
Therefore, the length of the base of the parallelogram is,