Question

The graph below shows a system of equations:

Part A: Write the equation of each line in slope-intercept form.
Line P:
Line Q:
Part B: What is the solution to the system?

Answer 1

Slope-intercept form is:

y = mx + b

"m" is the slope, "b" is the y-intercept (the y value when x = 0)

You can find the slope either by using the slope formula and finding 2 points:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

Or you can use this:

`slope=(rise)/(run)`

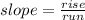
Rise is the number of units you go up(+) or down(-)

Run is the number of units you go to the right

(I'm using rise/run) If you look at line P, from each point you go up 1 unit, and to the right 2 units. So your slope is 1/2. When x = 0, the y value is 6, so your y-intercept is 6.

Line P:
`y=(1)/(2)x + 6`

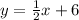
If you look at line Q, from each point you go down 4 units, and to the right 1 unit. So your slope is -4/1 or -4. When x = 0, the y value is -3, so your y-intercept is -3.

Line Q:
`y = -4x -3`

To find the solution to the system, you can find the point of intersection(the point where the lines meet). The point of intersection is (-2,5)

You can also do this by hand and set the equation of Line P and Q equal to each other to find x:

Line P: y = 1/2x + 6

Line Q: y = -4x - 3

1/2x + 6 = -4x - 3 Subtract 6 on both sides

1/2x = -4x - 9 Add 4x on both sides

1/2x + 4x = -9 Make the denominators the same

1/2x + 8/2x = -9

9/2x = -9 Multiply 2/9 on both sides to get x by itself

`((2)/(9)) (9)/(2)x = -9((2)/(9) )`

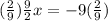
x = -2

Plug in -2 for x into either the equation of Line P or Line Q

y = -4x - 3

y = -4(-2) - 3

y = 8 - 3

y = 5

(-2,5)

Answer 2

Part A) line Q) y=-4x-3 and line P) y=1/2x +6

Part B) solution) x= -2 and y = 5