Question

Find the product of (5.2 · 10^-6) and (8 · 10^3).

A) 416 · 106-4
B) 4.16 · 10^-2
C) 41.6 · 10^-3
D) 0.416 · 10^-1

Answer 1

`\displaystyle\\(5.2\cdot10^(-6))*(8\cdot10^3)=\\\\=\underbrace{5.2*8}_(41.6)*\underbrace{10^(-6)*10^(3)}_(10^(-6+3))=\\\\=41.6*10^(-6+3)=\boxed{\bf41.6*10^(-3)}\\\\\texttt{Correct answer:}~~\boxed{\bf C)}`

Answer 2

Answer: B)
`4.16\cdot10^(-2)`

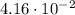
Explanation:

The given product :
`(5.2\cdot10^(-6))\cdot (8\cdot10^3)`

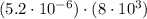
First open parenthesis :

`5.2\cdot10^(-6)\cdot 8\cdot10^3`

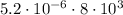
Write decimal values together and power of 10s together.

`5.2\cdot 8\cdot10^(-6)\cdot10^3`

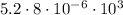
Using Law of exponent :
`a^m\cdot a^n= a^(m+n)`

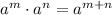
The above expression becomes.

`41.6\cdot10^(-6+3)=41.6*10^(-3)`

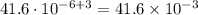
In scientific notation, the decimal must be placed after one digit (from left).

`41.6*10^(-3)=4.16*10*10^(-3)\\\\=4.16\cdot10^(-3+1)\\\\=4.16\cdot10^(-2)`

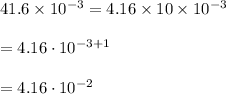
Hence, the correct answer is B)
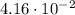`4.16\cdot10^(-2)` .