Answer:
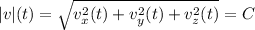

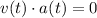
Step-by-step explanation:
Let's start with the definition of a constant velocity.
If the velocity magnitude, in three dimensions, is a constant value (C) we have a constant velocity, which means.
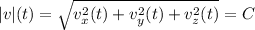
Now, we know that the dot product between v(t) and v(t) is the |v|².
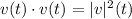
If we take the derivative whit respect to time in both sides of this equation we will have:
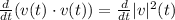
We apply the product rule on the left side and the right side will zero because the derivative of a constant is 0.


We know that dv(t)/dt = a(t) (using the acceleration definiton)
Therefore, we conclude:
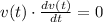
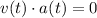
If the dot product is 0, it means that v(t) and a(t) are orthogonal.
I hope it helps you!