Question

A line with a slope of -3 and an x-intercept of 15 passes through which following points?

a. (0,30)
b. (5,15)
c. (10,10)
d. (-5,60)

Answer 1

Let's first write down all the information given in y = mx + b form. Notice that x-intercept means that y = 0 at that point. b is not given, so:

`0 = -3(15) + b`

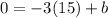
Let's solve for b:

`0 = -45+b`

`b = 45`

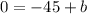
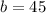
Now we have the equation:

`y = -3x + 45`

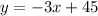
We can plug in every option given to see which choice makes it true:

(0, 30)

`30 = -3(0) + 45`

`30 \\eq 45`

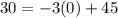
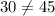
(5, 15)

`15 = -3(5) + 45`
`15 = -15+45`

`15\\eq 30`

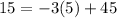
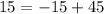
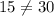
(10, 10)

`10 = -3(10) + 45`

`10 \\eq 15`

(-5, 60)

`60 = -3(-5) + 45`

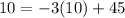
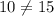
`60 = 60`

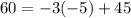
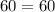
Therefore, choice D or (-5, 60) is your answer. Hope I could help! :)

*There is probably an easier way to solve this, I just didn't see it when I attacked the problem! :)