Answers: sin(A+B)=
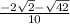 , cos(A+B)=
, cos(A+B)=
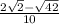 , A+B=Quadrant 3, sin(2A)=
, A+B=Quadrant 3, sin(2A)=
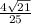
NOTES:
sin A =
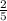 ⇒ cos A =
⇒ cos A =
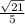
since tan B = 1 and is in Quadrant 3, then
sin B =
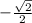 and cos B =
and cos B =
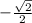
SIN (A + B):
sin (A + B) = (sin A * cos B) + (cos A * sin B)
= (
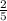 )(
)(
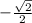 ) + (
) + (
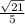 )(
)(
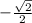 )
)
=
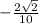 +
+
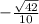
=
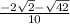
COS (A + B):
cos (A + B) = (cos A * cos B) - (sin A * sin B)
= (
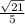 )(
)(
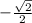 ) - (
) - (
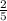 )(
)(
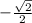 )
)
=
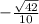 -
-
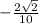
=
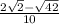
SIN 2A:
sin (A + A) = 2 (sin A * cos A)
= 2 (
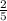 )(
)(
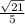 )
)
=
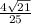
A + B:
sin A =
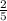
A = sin⁻¹
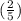
A = 23.57°
tan B = 1
B = tan⁻¹(1)
B = 45°
= 45° + 180° in Quadrant 3
= 225°
A + B = 23.6° + 225°
= 248.6° which lies in Quadrant 3