Question

angle A and angle B are complementary, that is their measurements add up to 90. Angle B measures 32 more than angle A. what are the measurements of the two angles?

Answer 1

Complementary= 90 Degrees

Equation: x + x = 90

A = x

B = x + 32

2x = 90 - 32

2x = 58

x = 29

Angle A = 29 degrees

Angle B = 61 degrees.

Answer 2

Answer: Two measurements are 29° and 61° .

Explanation:

Since we have given that

∠A and ∠B are complementary angles.

So, sum of ∠A and ∠B is 90°

so, our equation becomes,

`\angle A+\angle B=90^\circ--------(1)`

And according to question, it becomes,

`\angle B-\angle A=32^\circ\\\\\angle B=32^\circ+\angle A------(2)`

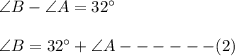
By putting the value of Eq(2) in Eq(1), we get that

`\angle A+\angle B=90^\circ\\\\\angle A+32^\circ+\angle A=90^\circ\\\\2\angle A+32^\circ=90^\circ\\\\2\angle A=90^\circ-32^\circ\\\\2\angle A=58^\circ\\\\\angle A=(58)/(2)=29^\circ`

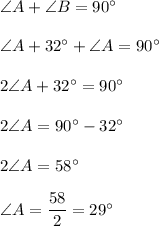
So, ∠A = 29°

and ∠B = 90° - 29° = 61°

Hence, two measurements are 29° and 61° .