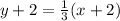Answer:
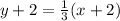
Explanation:
Pre-Solving
We are given that a line has a slope (m) of
 and passes through (-2, -2). We want to write this equation in point-slope form.
and passes through (-2, -2). We want to write this equation in point-slope form.
Point-slope form is given as
 where m is the slope and
where m is the slope and
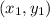 is a point.
is a point.
Solving
We can substitute what we know into the equation.
First, substitute
 as m.
as m.
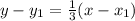
Now, substitute -2 as
 and -2 as
and -2 as
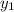 .
.
We get:
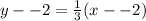
Simplify.