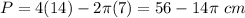a. i. Calculate the area of the complete semicircunference, and substract the area of both internal semicircunference.
Let A the area that we need to calculate, let B the area of the total semicircunference, and C the sum of the internal semicircunferences.
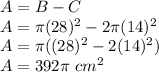
a. ii. The same idea. Let P the perimeter that we need to calculate, and let P' the perimeter of the total semicircunference, and Q the sum of the perimeters of the internal semicircunferences.
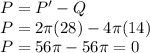
b. i
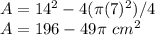
b. ii