Question

Let f(x) = 2(3)^(x+1) +4.

The graph of f(x) is stretched vertically by a factor of 2 to form the graph of g(x) .

What is the equation of g(x)?

Enter your answer in the box.

g(x) = ?

Answer 1

The equation of g(x) is:

`g(x)=4* 3^(x+1)+8`

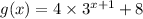
Explanation:

We are given a function f(x) as:

`f(x)=2* 3^(x+1)+4`

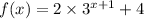
now we are given a condition that the graph of f(x) is stretched vertically by a factor of 2 to form the graph of g(x).

Now we know that for any initial function f(x) if the function is stretched vertically by a factor "a" to form the other function g(x) then the equation of the resultant function is given by:

`g(x)=a f(x)`

now here
`a=2`

and
`f(x)=2* 3^(x+1)+4`

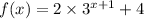
Hence, the resultant function g(x) is given by:

`g(x)=2* (2* 3^(x+1)+4)`

`g(x)=4* 3^(x+1)+8`

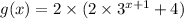
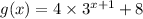
Hence, the equation of g(x) is:

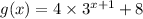`g(x)=4* 3^(x+1)+8`.

Answer 2

`g(x)=4(3)^(\left(x+1\right))+8`

Explanation:

Given equation is:

`f(x)=2(3)^(\left(x+1\right))+4`

Now it says that graph of f(x) is stretched vertically by a factor of 2 to form the graph of g(x).

Now we need to find about what is the equation of g(x).

We know that if function f(x) is stretched vertically by a factor of "a" then we get a*f(x)

Here factor is 2

So we just need to multiply g(x) with 2.

g(x)=a*f(x)

g(x)=2*f(x)

`g(x)=2\left(2(3)^(\left(x+1\right))+4\right)`

`g(x)=4(3)^(\left(x+1\right))+8`

Hence final answer is:

`g(x)=4(3)^(\left(x+1\right))+8`