Question

Prove that a triangle with two congruent altitudes is isosceles triangle. Write the complete proof in your paper homework and for online (only) respond to questions or statements (if any) that are parts of your proof or related to it.

Answer 1

Let PQR be a triangle with altitudes PS and QT of equal length(as altitude are congruent) as shown below in the figure.

Consider the triangles PSR and QTR

As, they are right triangles with the common angle i.e,
`\angle PRQ`

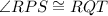`\angle RPS \cong RQT` {as the complementary angles to the angle PRQ}

`PS \cong RT` [side] [given]

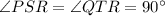`\angle PSR = \angle QTR = 90^(\circ)` [Angle]

`\angle RPS = \angle RQT` [Angle]

ASA Postulate (Angle-Side-Angle) states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.

Then; by ASA postulates;

`\triangle PSR \cong \triangle QTR`

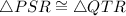
By CPCT[Corresponding Part of Congruent Triangles are equal]

`PR = QR`

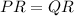
By definition of isosceles triangle;

⇒ ΔPQR is isosceles triangle hence proved!