Question

Need some pre-cal help.

Answer 1

c = number of children

s = number of students

a = number of adults

since the theater has a capacity of 189, then c + s + a = 189.

there are half as many "a" as "c", so then a = c/2 or 2a = c.

so the cost for all children since the price for one is 5 bucks, the total will be 5*c or 5c.

likewise, the total cost for students is 7*s or 7s.

and for adults likewise is 12*a or 12a.

we know all ticket sales was 1372, so then 5c + 7s + 12a = 1372.

`\bf \begin{cases} c+s+a=189\\ 5c+7s+12a=1372\\ 2a=\boxed{c} \end{cases}\qquad \implies \qquad \begin{cases} \boxed{2a}+s+a=189\\\\ 5\left( \boxed{2a} \right)+7s+12a=1372 \end{cases} \\\\\\ \begin{cases} 3a+s=189\\ 22a+7s=1372 \end{cases}`

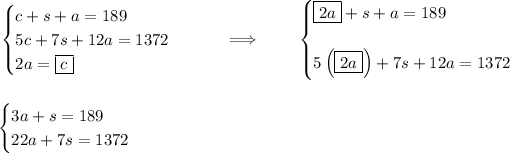
now, let's use the elimination method on that system of equations of two variables, let's multiply hmmmm say the first equation by -7, to eliminate the "s".

`\bf \begin{array}{llll} 3a+s=189&* -7\implies &-21a-7s=-1323\\ 22a+7s=1372&&~~22a+7s=1372\\ \cline{3-3} &&~~ ~~ a+~~0=49 \end{array} \\\\\\ a=49\qquad \qquad \stackrel{\textit{recall c = 2a}}{c=98} \\\\\\ \stackrel{\textit{and plugging \underline{a} in the 1st equation}}{3(49)+s=189}\implies 147+s=189\implies s=42 \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill a=49\qquad c=98\qquad s=42~\hfill`