Question

Please help me answer please. Thanks.

Answer 1

When it gives you a set of points of a function, and is asking for the original function, you are going to want to "plug in" the x-values and see if the y-values are produced.

For example, let's start with
`f(x) = (x + 1)^2`.

`(0 + 1)^2 \stackrel{?}{=} 1`

`1^2 \stackrel{?}{=} 1`

`1 = 1 \,\,\checkmark`

`(1 + 1)^2 \stackrel{?}{=} 4`

`2^2 \stackrel{?}{=} 4`

`4 = 4 \,\,\checkmark`

`(2 + 1)^2 \stackrel{?}{=} 9`

`3^2 \stackrel{?}{=} 9`

`9 = 9 \,\,\checkmark`

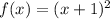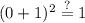
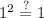
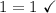
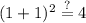
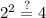
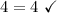
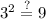
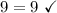
You can see that all of the points checked out for the first function, meaning that that is our answer. However, to be sure, let's quickly check over the other choices.

`f(x) = 4^x`

`f(0) = 4^0 = 1 \,\,\checkmark`

`f(1) = 4^1 = 4 \,\,\checkmark`

`f(2) = 4^2 = 16 \\eq 9`

• 
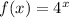
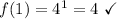
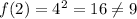
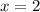  `x = 2` does not check out when used in the second answer choice

`f(x) = 3x + 1`

`f(0) = 3(0) + 1 = 1 \,\,\checkmark`

`f(1) = 3(1) + 1 = 4 \,\,\checkmark`

`f(2) = 3(2) + 1 = 7 \\eq 9`

• 
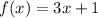
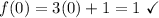
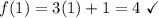
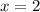  `x = 2` does not check out when used in the third option choice

`f(x) = 5x - 1`

`f(0) = 5(0) - 1 = -1 \\eq 1`

• 
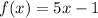
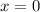  `x = 0` does not check out in the fourth equation

Thus, our answer remains as the first choice, or f(x) = (x + 1)².

Answer 2

f(x) = (x + 1)²

To determine which equation fits the given coordinate point, substitute the x-coordinates of the points into f(x) and if the value agrees with the y-coordinates of all 3 points then that is f(x)

1 f(x) = (x + 1)²

f(0) = 1² = 1 → (0, 1)

f(1) = 2² = 4 → (1, 4)

f(2) = 3² = 9 → (2, 9)

Hence f(x) = (x + 1)²

If you wish you can do the same test on the others to show they are not the required f(x)