Given:
Two triangles are given in the figure.
To find:
The m∠K and m∠J.
Solution:
In triangle FHK and IGJ,
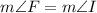 [Given]
[Given]
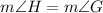 [Given]
[Given]
Two corresponding angles are equal. So,
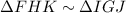 [By AA similarity theorem]
[By AA similarity theorem]
All corresponding angles of similar figures are same.
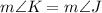 ...(i)
...(i)
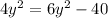
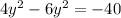
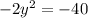
Divide both sides by -2.
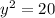 ...(ii)
...(ii)
Taking square root on both sides.
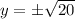
Now,
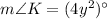
![m\angle K=[4(20)]^\circ](https://img.qammunity.org/2022/formulas/mathematics/high-school/pqvw7pa4qsp4ttgadx27h378kn52ca8bdy.png) [Using (ii)]
[Using (ii)]
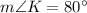
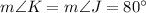 [Using (i)]
[Using (i)]
Therefore, the m∠K is 80° and m∠J is 80°.