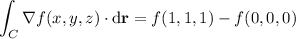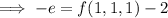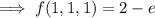Question

Suppose that \\abla f(x,y,z) = 2xyze^{x^2}\mathbf{i} + ze^{x^2}\mathbf{j} + ye^{x^2}\mathbf{k}. if f(0,0,0) = 2, find f(1,1,1). hint: as a first step, define a path from (0,0,0) to (1, 1, 1) and compute a line integral.

Answer 1

The simplest path from (0, 0, 0) to (1, 1, 1) is a straight line, denoted
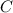`C`, which we can parameterize by the vector-valued function,

`\mathbf r(t)=(1-t)(\mathbf i+\mathbf j+\mathbf k)`

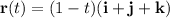
for
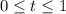`0\le t\le1`, which has differential

`\mathrm d\mathbf r=-(\mathbf i+\mathbf j+\mathbf k)\,\mathrm dt`

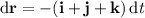
Then with
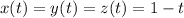`x(t)=y(t)=z(t)=1-t`, we have

`\displaystyle\int_(\mathcal C)\\abla f(x,y,z)\cdot\mathrm d\mathbf r=\int_(t=0)^(t=1)\\abla f(x(t),y(t),z(t))\cdot\mathrm d\mathbf r`

`=\displaystyle\int_(t=0)^(t=1)\left(2(1-t)^3e^((1-t)^2)\,\mathbf i+(1-t)e^((1-t)^2)\,\mathbf j+(1-t)e^((1-t)^2)\,\mathbf k\right)\cdot-(\mathbf i+\mathbf j+\mathbf k)\,\mathrm dt`

`\displaystyle=-2\int_(t=0)^(t=1)e^((1-t)^2)(1-t)(t^2-2t+2)\,\mathrm dt`

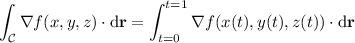
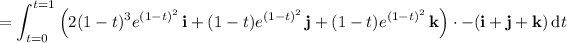
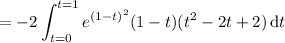
Complete the square in the quadratic term of the integrand:
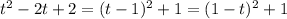`t^2-2t+2=(t-1)^2+1=(1-t)^2+1`, then in the integral we substitute
`u=1-t`:

`\displaystyle=-2\int_(t=0)^(t=1)e^((1-t)^2)(1-t)((1-t)^2+1)\,\mathrm dt`

`\displaystyle=-2\int_(u=0)^(u=1)e^(u^2)u(u^2+1)\,\mathrm du`

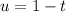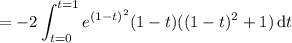
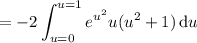
Make another substitution of
`v=u^2`:

`\displaystyle=-\int_(v=0)^(v=1)e^v(v+1)\,\mathrm dv`

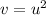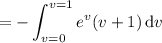
Integrate by parts, taking

`r=v+1\implies\mathrm dr=\mathrm dv`

`\mathrm ds=e^v\,\mathrm dv\implies s=e^v`

`\displaystyle=-e^v(v+1)\bigg|_(v=0)^(v=1)+\int_(v=0)^(v=1)e^v\,\mathrm dv`

`\displaystyle=-(2e-1)+(e-1)=-e`

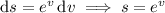
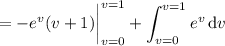
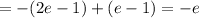
So, we have by the fundamental theorem of calculus that

`\displaystyle\int_C\\abla f(x,y,z)\cdot\mathrm d\mathbf r=f(1,1,1)-f(0,0,0)`

`\implies-e=f(1,1,1)-2`

`\implies f(1,1,1)=2-e`