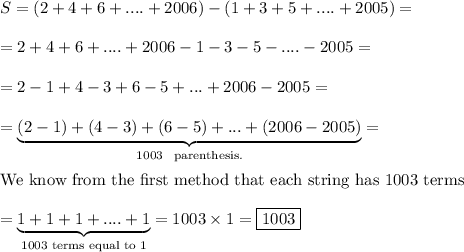Question

(2+4+6+....+2006)-(1+3+5+....+2005) the ‘....’ means they add up until it gets to 2006 or 2005. Plz tell me how you get the answer. I have the answer 1003 but I’m not sure how.Thanks!

Answer 1

I will solve the problem by 2 methods.

Method 1 to solve:

I will use Gauss's formula for calculating each string, then we will decrease the results.

We find the number of terms of each string.

`\displaystyle\\n_1=(2006-2)/(2)+1=(2004)/(2)+1=1002+1=1003~~\text{terms}\\ \\n_2=(2005-1)/(2)+1=(2004)/(2)+1=1002+1=1003~~\text{terms}\\\\n_1=n_2=n=1003~~\text{terms}\\\\\implies~~~\text{The two strings have the same number of terms.}\\\\S_1 =2+4+6+...+2006=(n(2006+2))/(2)=(1003*2008)/(2)=1003*1004\\ \\S_2=1+3+5+...+2005=(n(2005+1))/(2)=(1003*2006)/(2)=1003*1003\\\\S_1-S_2=1003*1004-1003*1003=1003(1004-1003)=1003*1=\boxed{1003}`

Method 2 to solve:

We intersect the terms in the second string among the terms of the first string.

`\displaystyle\\S=(2+4+6+....+2006)-(1+3+5+....+2005)=\\\\=2+4+6+....+2006-1-3-5-....-2005=\\\\=2-1+4-3+6-5+...+2006-2005=\\\\=\underbrace{(2-1)+(4-3)+(6-5)+...+(2006-2005)}_{1003~~\text{parenthesis.}}=\\\\\text{We know from the first method that each string has 1003 terms}\\\\=\underbrace{1+1+1+....+1}_{\text{1003 terms equal to 1}} = 1003 * 1 =\boxed{1003}`