Question

Reggie currently has a square rug in his living room. He is moving soon and has determined that for his new living room, he will need a rug that has a width that is two feet shorter than his current rug and a length that is five feet longer than his current rug. Let x represents the side measure of Reggie's current rug, in feet. Determine the equation that represents the area, y, in square feet, of the rug needed for his new living room.

y = x2 + 3x - 10


y = x2 - 7x + 10


y = x2 - 3x - 10


y = x2 + 7x + 10

Answer 1

Greetings!

Answer:

y =
`x^(2) + 3x - 10`

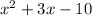
Explanation:

Because Reggies rug is square, this means that there is a constant, x, that stays the same, because x * x = area of square

The new rug is 2 feet shorter than his current one, so this would be (x - 2). As the rug is also 5 feet longer than his current one, this would make it (x + 5).

To find the equation that represents the area, the area needs to be found using

Length x Width = Area

So simply plug the values into this equation:

(x - 2)(x + 5) = area

= (x * x) + (x * 5) + (-2 * x) + (-2 * 5)

=
`x^(2) + 5x + -2x + -10`

A plus and a minus makes a negative:

`x^(2) + 5x  -2x  -10`

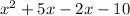
5x - 2x = 3x

So this would result in the end answer being:

`x^(2) + 3x - 10`

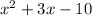
Hope this helps!