Question

A square has a side length x cm and area A cm2.

The area is increasing at a constant rate of 0.03 cm2s-1.

Find the rate of increase of x when A=25.

(Please solve and explain?)

Answer 1

The rate of increase of x when A = 25 is 0.0006 cm/s.

Explanation:

Area of a square A =
`x^(2)` sq. cm

So, x =
`√(A)` cm

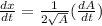`(dx)/(dt) =(1)/(2√(A) ) ((dA)/(dt) )` --- (1)

It is given that the area is increasing at the rate of 0.03
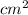`cm^(2)`/s.

Therefore,

`(dA)/(dt) =0.03 cm^(2) /s`

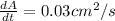
We need to find the rate of increase of x when A = 25.

Now, substituting the values of A and
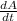`(dA)/(dt)`, (1) becomes

`(dx)/(dt) =(1)/(2√(25) ) (0.03)`

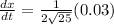
= 0.0006

Hence, the rate of increase of x when A = 25 is 0.0006 cm/s.