Question

A control gate in the form of a parabolic segment of base 12 and height 4 is submerged in water so that its base is 2 units below the surface of the water, as shown in Examination Figure I. Find the horizontal force on the gate if the density of the water is w.

Answer 1

The horizontal force on the gate is
`(576wg)/(5)`

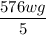
Solution-

From hydrostatics we know that,

Total force on a submerged gate is the product of pressure at the centroid of the gate and the area of the parabolic gate.

i.e
`F=P_(Centroid)* A`

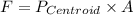
The centroid of the parabola is at
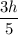`(3h)/(5)` along the vertical center line.

As the height of the parabola is given as 4, so the centroid will be at,
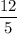`(12)/(5)` from the centre O.

As the gate is in the water, so the distance of the centroid from the surface of the water is

`=2+(4-(12)/(5))=(18)/(5)`

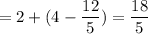
We know that,

`P_(Centroid)=h_(Centroid)* \rho * g`

`=(18)/(5)* w * g`

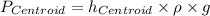
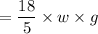
Area of the parabola is,

`A=(4ah)/(3)`

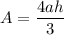
where,

a is the half distance, i.e from centre to the extreme point.

Here a = 6-0 = 6

So, Area of the parabola is
`(4* 6* 4)/(3)=32`

Putting all the values,

`F=(18)/(5)* w * g* 32=(576wg)/(5)`