Question

Scores on a test are normally distributed with a mean of 70 and a standard deviation of 11.5. find p81, which separates the bottom 81% from the top 19%.

Answer 1

Answer: The score p81 that separates the bottom 81% from the top 19% is 80.12

Step by step:

First, calculate the "z" value. Z is a normally distributed random variable with 0 mean and standard deviation 1. The score value corresponding to the desired percentile p81 can be determined from a z value as follows:

`z=(s-\mu)/(\sigma)\\z_(p81)=(p_(81)-70)/(11.5)\\\implies p_(81)=z_(p81)\cdot 11.5+70`

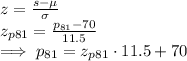
We use a z-table (check online) to find the z value for the 81-st percentile. I found
`z_(p81)=0.88` and so we use that value to calculate the score for the percentile:

`p_(81)=0.88\cdot 11.5+70=80.12`

The score p81 that separates the bottom 81% from the top 19% is 80.12