Question

Let f(x) = 7x + 12 , f ^ -1 (x) =

Answer 1

To find the inverse function we must admit that f(x) = x and x = y. That is

`\mathsf{x=7y+12}`

Now, we need to isolate the y

`\mathsf{7y=x-12}\\\\\\\mathsf{y=(x-12)/(7) }`

Like this

`\mathsf{f^(-1)(x)=(x-12)/(7)}`

Hope this helps, good studies.

Answer 2

To find an inverse, we can follow these steps:

1. set f(x) equal to y.
2. solve for x
3. switch the x and y
4. set y equal to f^-1 (x) and you have your answer.

Let's follow these steps:

`f(x) = 7x+12=y`

`y = 7x+12`

`y-12=7x`

`x = (y-12)/(7)`

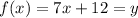
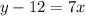
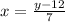
Now, we switch the y and the x:

`y = (x-12)/(7)`

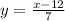
And set that equal to f^-1(x). Therefore, your answer is:

`f^(-1)(x) = (x-12)/(7)`

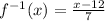
Hope I could help you Jermaine! :)