Answer:
Proportional relationship states that one in which two quantities vary directly with each other.
In other words, we say the variable y varies directly as x if:
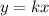 , where k is constant of proportionality.
, where k is constant of proportionality.
(1)
Given: y and x varies a proportional relationship, and y = 7 and x=2
find the value of x when y =21
By the definition of proportional relationship;
y = kx ......[1]
Substitute the value y= 7 and x = 2 to solve for k;
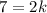
Divide by 2 to both sides we get;
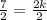
Simplify:
k = 3.5
Now, substitute the value of k = 3.5 and y =21 in equation [1] to find the value of x.
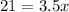
Divide both sides by 3.5 we get;
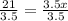
Simplify:
x = 6
Therefore, the value of x is 6.
(2)
Given: y and x varies a proportional relationship, and y = 9 and x=2
find the value of y when x=3.
By the definition of proportional relationship;
y = kx ......[1]
Substitute the value y= 9 and x = 2 to solve for k;
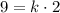
Divide by 2 to both sides we get;

Simplify:
k = 4.5
Now, substitute the value of k = 4.5 and x=3 in equation [1] to find the value of y.
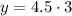
Simplify:
x = 13.5
Therefore, the value of y is 13.5.
(3)
From the given table,
y = 2.8 when x = 2
by the definition of proportional relationship;
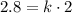
or
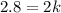
Divide by 2 to both sides, we get;
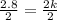
Simplify:
k = 1.4
Therefore, the equation that represents the table is; y = 1.4 x