Question

5. (05.03 LC) What is the simplified form of the quantity of x plus 5, all over the quantity of 3x plus 4 + the quantity of x plus 4, all over the quantity of x plus 3 ? (2 points)

A) the quantity of 2x plus 9, all over the quantity of 4x plus 7
B) the quantity of 4x squared plus 24x plus 31, all over the quantity of 3x squared
plus 13x plus 12
C) the quantity of 4x squared plus 24x plus 31, all over the quantity of 4x plus 7 D) the quantity of 2x plus 9, all over the quantity of 3x squared plus 13x plus 12

Answer 1

B.
`(4x^(2)+24x+31)/(3x^(2)+13x+12)`

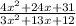
Step-by-step explanation:

We have been given a rational expression
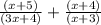`((x+5))/((3x+4))+((x+4))/((x+3))` and we are asked to simplify our rational expression.

We can see that our denominators are not equal. Since the two denominators do not share any common factors, the common denominator is simply the product of these two denominators.

To keep the value of expression same we will multiply the same quantity with numerators and denominators.

`((x+5)(x+3))/((3x+4)(x+3))+((x+4)(3x+4))/((x+3)(3x+4))`

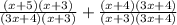
Now let us simplify our expression using FOIL.

`(x^(2)+3x+5x+15)/(3x^(2)+9x+4x+12)+(3x^2+4x+12x+16)/(3x^(2)+4x+9x+12)`

`(x^(2)+8x+15)/(3x^(2)+13x+12)+(3x^2+16x+16)/(3x^(2)+13x+12)`

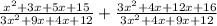
Now we have same denominators, so we can add our numerators.

`(x^(2)+8x+15+3x^2+16x+16)/(3x^(2)+13x+12)`

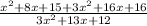
Now let us combine like terms.

`((1+3)x^(2)+(8+16)x+15+16)/(3x^(2)+13x+12)`

`(4x^(2)+24x+31)/(3x^(2)+13x+12)`

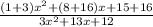
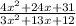
Therefore, the simplest form of our given rational expression will be
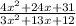`(4x^(2)+24x+31)/(3x^(2)+13x+12)` and option B is the correct choice.