Answer:
34 mph.
Explanation:
Let x be speed of Charlene, then speed of Paul will be x+16 as we are given that Paul is driving 16 mph faster than Charlene.
Let y be distance covered by Charlene, then distance covered by Paul will be 420-y.
Now we will use formula
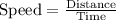 . Upon using our given information we will get two equation and two unknowns as:
. Upon using our given information we will get two equation and two unknowns as:

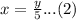
Upon substituting
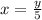 in 1st equation we will get,
in 1st equation we will get,
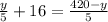
Upon multiplying both sides of our equation by 5 we will get,
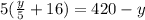
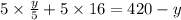
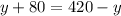

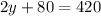
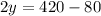
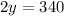
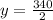
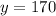
Upon substituting y=170 in 2nd equation we will get,
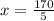
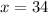
Therefore, Charlene's speed is 34 miles per hour.