Question

I need help with this word problem please

Answer 1

Explanation:

Given function is,

f(x) =
`x√(x)`

We can rewrite this function as,

f(x) =
`x^{(3)/(2)}`

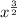
a). Domain of the function is [0, ∞)

Derivative of the function in this domain,

f'(x) =
`(3)/(2)x^{((3)/(2)-1)}`

=
`(3)/(2)x^{(1)/(2)}`

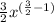
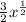
Since, f'(x) > 0 in the interval [0, ∞)

Function is increasing in the interval [0, ∞)

b). For local maxima and local minima,

Second derivative of the function,

f"(x) =
`(3)/(2)((1)/(2))x^{(1)/(2)-1}`

=
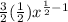
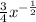`(3)/(4)x^{-(1)/(2)}` > 0

So the function should have a local minima.

But the function is continuous in the interval x ≥ 0,

There is no local minima (only absolute minima).

c). Since, second derivative is undefined at x = 0,

There are no inflection points.

d). Since, f"(x) > 0 in the interval [0, ∞)

Concavity of the curve is UPWARDS.