Let the width of the barn be = x feet
So length of the barn = 2x
Height of the barn = x-8
As the stalls are 6 feet longer from both ends hence, we have to find the area with width as x-12 feet
Volume of the space is = 3840 cubic feet
Hence, equation is :
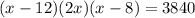
Solving this we get
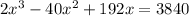

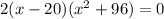
This gives x=20 and x= ±
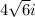
Hence, neglecting the square root value we get x = 20 feet
Hence, the width is = x-12 = 20 - 12 = 8 feet
Length is = 2x = 2*20 = 40 feet
Height is = x-8 = 20 - 8 =12 feet
And we can cross check this by multiplying all the three dimensions to get 3840 cubic feet
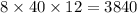 cubic feet.
cubic feet.