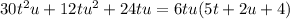ANSWER TO QUESTION 1
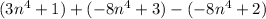
Let us expand the parenthesis first.
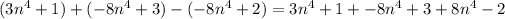
This will simplify to,
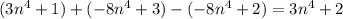
ANSWER TO QUESTION 2
We want to write
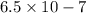
in standard notation.
Let us simplify first to obtain,
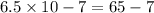
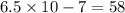
In standard notation we have,
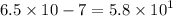
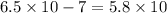
ANSWER TO QUESTION 3
This question requires us to write
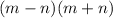
in words.
Subtract

from
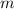
and multiply the result by the sum of
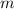
and

.
ANSWER TO QUESTION 4
We want to simplify
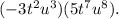
We use the laws of exponents to simplify the above expression.
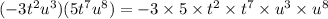
Recall that,
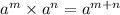
This implies that,
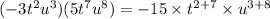
This simplifies to,
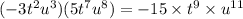
ANSWER TO QUESTION 5.
We want to complete the property of exponents given by,

According to this product property of exponents,since the bases are the same we write down one base and add the exponents to obtain,
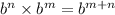
ANSWER TO QUESTION 6.
Please see attachment for the long division
ANSWER TO QUESTION 7.
We were given the expression,
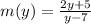
This is a rational expression. The expression is not defined for
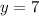
Therefore it is not possible to evaluate
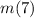
Evaluating this will result in division by zero as shown below.
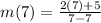
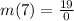
ANSWER TO QUESTION 8.
We want to factor the Greatest Common Factor out of
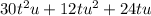
The greatest common factor is
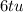
We factor it to obtain,