Question

F(x) = 4x - 1; g(x) = 5x ( to the second power).

Which expression is equal to (f o g)(x)?

A. 20x ( to the second power) - 1
B. 20x ( to the third power) - 5x ( to the second power)
C. 5x ( to the second power) + 4x - 1
D. 80x ( to the second power) -40x + 5

Answer 1

For this case we have that by definition, if we want to find (f o g) (x) we must replace g (x) in f (x), on the contrary, if we want to find (g o f) (x) we must replace f (x) in the function g (x).

So:

`(f o g) (x) = 4 (5x ^ 2) - 1\\(f o g) (x) = 20x ^ 2-1`

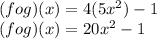
Thus, the expression that is equal to (f o g) (x) is
`20x ^ 2-1`, or 20x (to the second power) - 1

Answer:

Option A

20x (to the second power) - 1

Answer 2

(f o g)(x)=

stick g(x) in for x in the function f(x)

(f o g)(x)= 4(g(x)) -1

=4*5x^2 -1

= 20x^2 -1