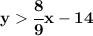Question

Adrianna is attempting to write an inequality from a graph. She knows that the dash boundary line passes through the points (27,10) and (-45,-54). She also notices that the point (0,0) is a solution to this inequality. If Adrianna must write the inequality in slope intercept from, what will she write?

Answer 1

we know the line passes through those points, so let's find the EQUATion of it firstly.

`\bf (\stackrel{x_1}{27}~,~\stackrel{y_1}{10})\qquad (\stackrel{x_2}{-45}~,~\stackrel{y_2}{-54}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{-54-10}{-45-27}\implies \cfrac{-64}{-72}\implies \cfrac{8}{9} \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-10=\cfrac{8}{9}(x-27) \\\\\\ y-10=\cfrac{8}{9}x-24\implies y=\cfrac{8}{9}x-14`

so, that's its EQUATion, now, we know the (0,0) is a solution of this inequality, namely the (0,0) point lies in the "true region" or will be the "shaded region" of the inequality, let's plug those values,

`\bf y=\cfrac{8}{9}x-14\implies \stackrel{\textit{using x = 0, y = 0}}{0=\cfrac{8}{9}(0)-14}\implies 0=-14`

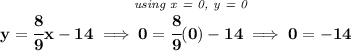
well, clearly 0 is not equals to -14.... we know 0 is greater, recall for the negative values, the farther from zero the smaller.

we also know that the line is dashed, meaning the borderline values are not included, so is either a > or <, thus since 0 > -14, then

`\bf y>\cfrac{8}{9}x-14`