Question

A 55kg skater spins at 12 m/s while carving a circle on the ice that has a radius of 6.0m. What net force must act on the skater to keep her in the circular path?

Answer 1

Answer: The force counteracting the centrifugal force must be 1320N. The net force acting in the radial direction will thus be 0. (see comment below)

Step-by-step explanation:

The force acting on the skater skating on a circular path is the centrifugal force. For the skater to stay on that path the blades must ensure sufficient "edge" to enact a counterforce of same magnitude but direction opposite to the centrifugal force.

The centrifugal force formula for this setting is as follows:

`F_c = (mv^2)/(r)`

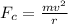
with m the mass, v the speed, and r the radius. Using values we are given, the force amounts to:

`F_c = (mv^2)/(r)=(55 kg\cdot 12^2 ((m)/(s))^2)/(6 m)=1320\,\,kg\cdot (m)/(s^2)`

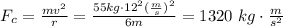
Comment:

I may be misunderstanding the question. The problem is likely asking for the force counteracting the centrifugal force, however, they use the term "net force" which I consider to be the result of adding the centrifugal and the force exerted on the skates' edges. That sum (in the radial direction) should be 0 if the skater is to stay in the path. You may be a better judge knowing your teacher.

As a side comment (opinion): the term "spin" implies rotation around own axis. So, in this context it is quite a misnomer. The skater surely is not spinning around her own axis while carving a circle as written in this problem.