Question

Four velcro-lined air-hockey disks collide with each other in a perfectly

inelastic collision. The first disk has a mass of 50.0 g and a velocity of
0.80 m/s to the west, the second disk has a mass of 60.0 g and a velocity of
2.50 m/s to the north, the third disk has a mass of 100.0 g and a velocity of
0.20 m/s to the east, and the fourth disk has a mass of 40.0 g and a
velocity of 0.50 m/s to the south. What is the final velocity of the disks
after the collision?

Answer 1

The final velocity of the disks after the inelastic collision can be calculated using the principle of conservation of momentum.

Step-by-step explanation:

The final velocity of the disks after the collision can be calculated using the principle of conservation of momentum. In an inelastic collision, the objects stick together after the collision. The total momentum before the collision is equal to the total momentum after the collision.

The momentum of an object is calculated by multiplying its mass by its velocity. The final velocity of the disks can be found by dividing the total momentum after the collision by the total mass of the objects.

In this case, the total mass of the objects is 50.0 + 60.0 + 100.0 + 40.0 = 250.0 g. Convert this to kilograms by dividing by 1000: 250.0 g = 0.25 kg.

The total momentum before the collision is: (50.0 g * 0.80 m/s) + (60.0 g * 2.50 m/s) + (100.0 g * 0.20 m/s) + (40.0 g * -0.50 m/s) = 105.0 kg·m/s.

Dividing the total momentum by the total mass gives the final velocity of the disks: 105.0 kg·m/s / 0.25 kg = 420.0 m/s.

Therefore, the final velocity of the disks after the collision is 420.0 m/s.

Answer 2

The magnitude of the final velocity is approximately 0.526 m/s in approximately the direction of 8.746° East of South

Step-by-step explanation:

The given collision parameters are;

The kind of collision experienced by the four velcro-lined air-hockey disk = Inelastic collision

The mass of the first disk, m₁ = 50.0 g

The velocity of the first disk, v₁ = 0.80 m/s West = -0.8·i

The mass of the second disk, m₂ = 60.0 g

The velocity of the second disk, v₂ = 2.50 m/s North = 2.5·j

The mass of the third disk, m₃ = 100.0 g

The velocity of the third disk, v₃ = 0.20 m/s East = 0.20·i

The mass of the fourth disk, m₄ = 40.0 g

The velocity of the fourth disk, v₄ = 0.50 m/s South = -0.50·j

Therefore, the total initial momentum of the four velcro-lined air-hockey disk,
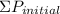`\Sigma P_(initial)` is given as follows;

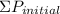`\Sigma P_(initial)` = m₁·v₁ + m₂·v₂ + m₃·v₃ + m₄·v₄ = 50.0×(-0.80·i) + 60.0×(2.50·j) + 100 × (0.20·i) + 40.0 × (-0.50·j)

∴
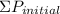`\Sigma P_(initial)` = -40·i + 150·j + 20·i - 20·j = -20·i + 130·j

∴
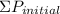`\Sigma P_(initial)` = -20·i + 130·j

By the law of conservation of linear momentum, we have;

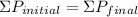`\Sigma P_(initial) = \Sigma P _(final)` = -20·i + 130·j

Therefore, given that the collision is perfectly inelastic, the disks move as one after the collision and the four masses are added to form one mass, "m", m = m₁ + m₂ + m₃ + m₄ = 50.0 + 60.0 + 100.0 + 40.0 = 250.0

∴ m = 250.0 g

Let, "v" represent the final velocity of the four disks moving as one after the collision

We have;

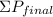`\Sigma P _(final)` = m × v = 250.0 × v = -20·i + 130·j

∴ v = -20·i/250 + 130·j/250 = -0.08·i + 0.52·j

The final velocity of the four disks after collision, v = -0.08·i + 0.52·j

The magnitude of the final velocity,
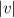`\left | v \right |` = √((-0.08)² + (0.52)²) ≈ 0.526

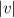`\left | v \right |` ≈ 0.526 m/s

The direction of the final velocity, θ = arctan(0.52/(-0.08)) ≈ -81.254°

The direction of the final velocity, θ ≈ -81.254° which is 8.746° East of South