Question

A (litres)

160
140
120
100
The amount of oil A left in a leaky barrel after
t minutes is shown on the graph alongside.
a Find the gradient and A-intercept of the line.
Interpret your answers.
6 Find the model connecting A and t.
c. How much oil will be left after 15 minutes?
d For what values of t is it reasonable to apply
this model?
80
60
40
20
0
12
6
(minutes)

Answer 1

Explanation:

Graph attached represents the relation between amount of oil left in the leaky oil tanker and time.

a). Gradient of the line =
`\frac{\text{Rise}}{\text{Run}}`

=
`((160-120))/((0-8))`

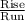
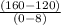
= -5

A-intercept = 160

b). Linear equation to represent the given relation in the graph will be,

A = (-5)t + 160

c). At t = 15 minutes,

A = (-5)(15) + 160

A = -75 + 160

A = 85 liters

d). This model is applicable till the container gets fully emptied.

For A = 0,

0 = -5t + 160

t =
`(160)/(5)`

t = 32 minutes

Therefore, this model is reasonable up to t = 32 minutes.