Question

A.) a. SSS; b. SAS

B.) a. SSS; b. CPCTC

C.) a. SAS; b. CPCTC

D.) a. ASA; b. HL

Answer 1

a. SSS; b. CPCTC ⇒ answer B

Explanation:

* Lets explain how to solve the problem

- In the two triangles ABC and FED

∵ AD = FC ⇒ given

- By adding the common part DC to them

∴ AC = FD ⇒ (1)

∵ BC = ED ⇒ (2) (given)

- We can find the length of AB and FE by using the rule of the distance

`d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`

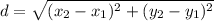
∵ A = (0 , 0) , B = (1 , 3)

∴ AB =
`\sqrt{(1-0)^(2)+(3-0)^(2)}=√(1+9)=√(10)`

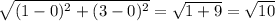
∵ F = (8 , 4) , E = (7 , 1)

∴ FE =
`\sqrt{(7-8)^(2)+(1-4)^(2)}=√(1+9)=√(10)`

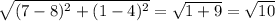
∴ AB = FE = √10 ⇒ (3)

- From (1) , (2) , (3)

∴ Δ ABC ≅ Δ FED by SSS

- The meaning of CPCTC is corresponding parts of congruent triangles

are congruent.

∴ By CPCTC ∠B = ∠E

* by (a) SSS, Δ ABC ≅ Δ FED, and then ∠B = ∠E by (b) CPCTC