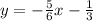Question

Write the slope-intercept form of the equation of the line through the given point with the

given slope.
through: (2,-2), slope = -5/6

Answer 1

`\rm y = -(5)/(6) x-(1)/(3)`

Explanation:

The slope intercept form of a line equation is

y = mx + b where m is the slope and b the y-intercept

Slope is given as
`- (5)/(6)`

So equation of line is

`\rm y = -(5)/(6)x + b\\\\We\;can\;find\;bby\;substituting\;the\;x,\;y\;values\;for\;point\;(2,\;-2)\;into\;the\;equation\\\rm y = -(5)/(6)x + b\\\\\\\rm We\;can\;find\;by\;substituting\;the\;x,\;y\;values\;for\;point\;(2,\;-2)\;into\;the\;equation\\\\-2 = -(5)/(6)*2 + b\\\\-2 = -(10)/(6) + b\\\\-2 = -(5)/(3) + b\\\\`

`\rm Adding\;(5)/(3) \;to\;both\;sides\;:\\(5)/(3) - 2 = b\\\\(5-6)/(3) = b\\\\b = -(1)/(3)`

So equation of line is

`\rm y = -(5)/(6) x-(1)/(3)`

Answer 2

`\huge\boxed{y=-(5)/(6)x-(1)/(3)}`

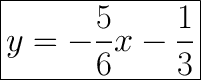
Useful Information:

The equation of a straight line:
`y=mx+c`

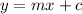
Explanation:

To work this out you would first need to substitute the gradient into the equation, this gives you
`y=-(5)/(6)x+c`.

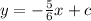The next step is to substitute the x and y coordinates from the point (2,-2) into the equation, this gives you
`-2=-(5)/(6)(2)+c`

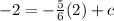
In order to work out the value of c, you would have to bring the value of
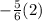`-(5)/(6)(2)` over to the other side, this can be done by adding
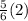`(5)/(6)(2)` or
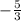`-(5)/(3)` to -2, which gives you
`-(1)/(3)`.

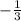The final step is to substitute the m value of
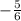`-(5)/(6)` and the c value of
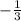`-(1)/(3)` into the equation, this gives you
`y=-(5)/(6)x-(1)/(3)`

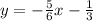
1) Substitute the gradient.

`y=-(5)/(6)x+c`

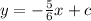
2) Substitute the x and y coordinates.

`-2=-(5)/(6)(2)+c`

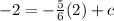
3) Bring
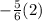`-(5)/(6)(2)` over to the other side.

`c=-2+(5)/(6)(2)`

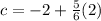
4) Simplify to find the value of c.

`c=-(1)/(3)`

5) Substitute the m and c values.

`y=-(5)/(6)x-(1)/(3)`