Question

The sides of a square are increased by a scale factor of 7. The perimeter of the smaller square is 16 ft. What is the perimeter of the larger square? A. 28 ft B. 56 ft C. 64 ft D. 112 ft

Answer 1

D. 112 ft

Explanation:

First, we consider the small square. We know that it has a perimeter of 16ft, and a square has equal sides. So:

`P = 16ft\\P = x + x + x + x = 4x\\4x=16\\x=(16)/(4) = 4`

This means that each side of the small square is 4 feet long. Then, the problem says that is increased by a scale factor of 7, this means that each side is multiplied by 7:

`BiggerSquareSide=4(7) = 28`

Now, we multiply by 4, that is, by each side of the bigger square:

`P_(bigger) = 28(4) = 112ft`

Therefore, the larger square has 112ft of perimeter.

Answer 2

D. 112 inches.

Explanation:

Let x be the side length of our smaller square.

Since we know that all sides of squares are of equal length and perimeter of square is 4 times the measure of its side length.

We have been given that perimeter of the smaller square is 16 ft. We can set an equation for the perimeter of our smaller square as:

`4x=16`

Let us solve for the side length of our smaller square by dividing both sides of our equation by 4.

`(4x)/(4) =(16)/(4)`

`x=(16)/(4)`

`x=4`

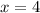
We can see that each side of smaller square measures 4 inches.

We have been given that sides of a square are increased by a scale factor of 7, therefore, each side length of larger square will be 7 times the side of smaller square.

`\text{Each side of larger square}=7*4=28`

Now let us find perimeter of the larger square by multiplying 28 by 4.

`\text{Perimeter of larger square}=28* 4=112`

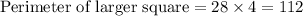
Therefore, the perimeter of larger square will be 112 inches and option D is the correct choice.