Question

what is the point slope form of the equation for the line with a slope of -8 that passes through the point (5, -3) ?

Answer 1

We know that the form of line passing through point (x₀ , y₀) and having slope m is :

`\clubsuit` y - y₀ = m(x - x₀)

Here the line passes through the point (5 , -3)

⇒ x₀ = -2 and y₀ = -5

Given : Slope(m) = -8

Substituting all the values in the standard form, We get :

Equation of the line : y + 3 = -8(x - 5)

Answer 2

The point slope form is
`y+3=-8(x-5)`

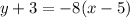
Step-by-step explanation

The point slope form of the equation of a straight line is given by the formula;

`y-y_1=m(x-x_1)`.

Where
`m` is the slope of the straight line and the point
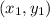`(x_1,y_1)` lies on the line.

We were given the slope to be
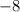`-8`. This means that
`m=-8`.

We were also given that the point
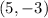`(5,-3)` lies on the line.

We substitute all these values in to the above equation to obtain,

`y--3=-8(x-5)`

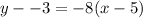
This simplifies to

`y+3=-8(x-5)`

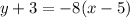
The correct answer is D