Question

what is the point slope of the equation for a line with a slope of 6/19 that passes through the point (-1 , 7/5) ?

Answer 1

Answer: Third option is correct.

Step-by-step explanation:

Since we have given that

Slope of line is given by

`(6)/(19)`

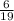
Passing through the point is given by

`(-1,(7)/(5))`

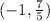
As we know the formula for "Point slope form" :

`(y-y_0)=m(x-x_0)`

So, we put the given value , such that

`(y-(7)/(5))=(6)/(19)(x+1)\\\\(5y-7)/(5)=(6x)/(19)+(6)/(19)\\\\19(5y-7)=5(6x+6)\\\\95y-133=30x+30\\\\95y-30x=30+133\\\\95y-30x=163`

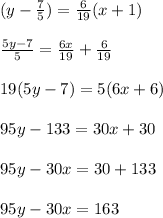
Hence, Third option is correct.

Answer 2

The point slope form is
`y-(7)/(5)=(6)/(19)(x+1)`

EXPLANATION

The point slope form of the equation of a straight line is given by the formula;

`y-y_1=m(x-x_1)`.

Where
`m` is the slope of the straight line and the point
`(x_1,y_1)` lies on the line.

We were given the slope to be
`(6)/(19)`. This means that
`m=(6)/(19)`.

We were also given that the point
`(-1,(7)/(5))` lies on the line.

We substitute all these values in to the above equation to obtain,

`y-(7)/(5)=(6)/(19)(x--1)`

This simplifies to

`y-(7)/(5)=(6)/(9)(x+1)`

The correct answer is C