Question

Which of the following shows a factor of 100b2 - 144a4? A. 10b - 12a B. 10b + 12a C. 10b + 12a2 D. 50b - 72a2

Answer 1

You may notice that the expression is a difference of squares, with
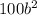`100b^2` as one of the squares and
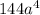`144a^4` as the other square.

Now, we can apply the Difference of Squares formula:

`a^2 - b^2 = (a - b)(a + b)`

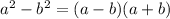
In this case, we can say
`a^2 = 100b^2` and
`b^2 = 144a^4`. We are going to need to find
`a` and
`b`. To do this, we can take the square root of both sides of the prior two equations.

`√(a^2) = √(100b^2)`

`a = 10b`

`√(b^2) = √(144a^4)`

`b = 12a^2`

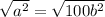
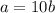
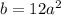
We can now use the equation to find our result:

`100b^2 - 144a^4 = (10b - 12a^2)(10b + 12a^2)`

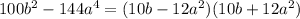
You can see that Choice C, or 10b + 12a² is a factor.