Question

Question is 15 points

Answer 1

sin(x+y)=sin(x)cos(y)-cos(x)sin(y)

also, remember pythagorean rule,
`sin^2(x)+cos^2(x)=1`

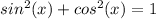
given that sin(Θ)=4/5 and cos(x)=-5/13

find sin(x) and cos(Θ)

sin(x)

cos(x)=-5/13

using pythagorean identity

(sin(x))^2+(-5/13)^2=1

sin(x)=+/- 12/13

in the 2nd quadrant, sin is positve so sin(x)=12/13

cos(Θ)

sin(Θ)=4/5

using pythagrean identity

(4/5)^2+(cos(Θ))^2=1

cos(Θ)=+/-3/5

in 1st quadrant, cos is positive

cos(Θ)=3/5

so sin(Θ+x)=sin(Θ)cos(x)+cos(Θ)sin(x)

sin(Θ+x)=(4/5)(-5/13)+(3/5)(12/13)

sin(Θ+x)=16/65

answer is 1st option