1.
A picture is shown of the graph of
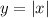 . To graph
. To graph
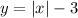 , we use the translation property of graphs. If
, we use the translation property of graphs. If
 is a function given, then
is a function given, then
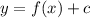 (c being a constant) will shift the curve c units up. Similarly if c is negative, it is going to shift the curve downwards c units. Hence, the graph of the function
(c being a constant) will shift the curve c units up. Similarly if c is negative, it is going to shift the curve downwards c units. Hence, the graph of the function
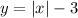 is
is
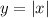 shifted 3 units down. Attached picture shows the new graph.
shifted 3 units down. Attached picture shows the new graph.
2.
Attached picture shows the parent function
 in blue and the new transformed function
in blue and the new transformed function
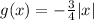 in red.
in red.
- The negative sign in front of
 reflects the line about the x axis.
reflects the line about the x axis. - The
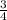 in front of the function makes the corresponding y values for all x less (
in front of the function makes the corresponding y values for all x less (
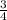 of all values in the original).
of all values in the original).
3.
For the given function
 , we write a general form of the absolute value function and identify the constants.
, we write a general form of the absolute value function and identify the constants.
General form,
](https://img.qammunity.org/2019/formulas/mathematics/high-school/8w5fpnf7ghpi6ap08nkz3l29ij2i904qtl.png) b|+c[/tex]
b|+c[/tex]
- If a is positive, graph opens upward and opens downward when a is negative.
- +b translates the original graph (
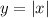 ) b units left and -b translates the original b units right
) b units left and -b translates the original b units right - +c translates the original graph c units up and -c translates it c units down
- Axis of symmetry is given as
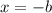
- Vertex is given as (-b,c)
As noted, we can now say that the vertex is
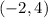 and axis of symmetry as
and axis of symmetry as
 .
.
As for transformations (comparing with parent function), we can note the following:
- reflected about x axis, opens downward
- translated 2 units left
- translated 4 units up
4.
From the vertex shown be know that this graph is translated 2 units left and 6 units down. So by using the properties noted above, we can write
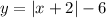 . But the graph, compared to the parent function
. But the graph, compared to the parent function
 ) is a little wider. So there is a value for a, the coefficient before the absolute value sign. To figure it out, we can take any 2 points on the graph and solve for a. Let us take a random point
) is a little wider. So there is a value for a, the coefficient before the absolute value sign. To figure it out, we can take any 2 points on the graph and solve for a. Let us take a random point
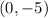 .
.
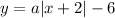 , pluggin 0 in x and -5 in y gives us,
, pluggin 0 in x and -5 in y gives us,
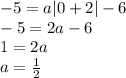 .
.
So our final equation is
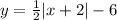
5.
From the equation we can make out that the graph is shifted 2 units left and 3 units down compared to the parent
 . Also, the 2 in front tells us all y values are twice of the original y values of the parent function for all values of x. Attached graph is shown.
. Also, the 2 in front tells us all y values are twice of the original y values of the parent function for all values of x. Attached graph is shown.