A differentiable function
 is increasing on an open interval
is increasing on an open interval
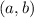 if
if
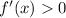 for all
for all
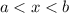 , and decreasing if
, and decreasing if
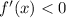 . For this problem, you then need to compute the derivative:
. For this problem, you then need to compute the derivative:

then solve for
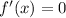 :
:
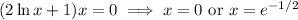
We can ignore
 because
because
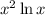 is defined only for
is defined only for
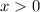 . So we have two intervals to consider,
. So we have two intervals to consider,
 and
and
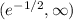 . All we need to do is pick any value from either interval and check the sign of the derivative
. All we need to do is pick any value from either interval and check the sign of the derivative
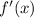 . Since
. Since
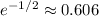 , from the first interval we can take
, from the first interval we can take
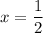 , and from the second we can pick
, and from the second we can pick
 .
.
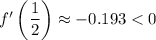
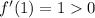
The above indicates that
 is decreasing on the first interval
is decreasing on the first interval
 , and increasing on the second interval
, and increasing on the second interval
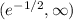 .
.
For part (b), we use the info from above as part of the first derivative test for extrema. We have one critical point at
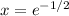 , and we know how
, and we know how
 behaves to either side of this point;
behaves to either side of this point;
 decreases to left of it, and increases to the right. This pattern is indicative of a minimum occurring at
decreases to left of it, and increases to the right. This pattern is indicative of a minimum occurring at
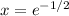 , and we find that
, and we find that
 has the (local) minimum value of
has the (local) minimum value of
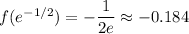 .
.