Question

Find the equation of the line parallel to 7y+2x-10=0 that passes through the point (2,2)

Answer 1

Parallel lines have the same slope.

We have the general form of line. Transform to the slope-intercept form:

`y=mx+b`

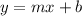
m - slope, b - y-intercept

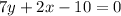`7y+2x-10=0` subtract 2x from both sides

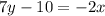`7y-10=-2x` add 10 to both sides

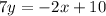`7y=-2x+10` divide both sides by 7

`y=-(2)/(7)x+(10)/(7)\to m=-(2)/(7)`

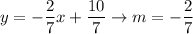
Therefore we have:
`y=-(2)/(7)x+b`.

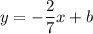The line passes through the point (2, 2). Substitute the coordinates of the point to the equation of a line:

`2=-(2)/(7)(2)+b`

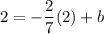
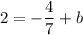`2=-(4)/(7)+b` add
`(4)/(7)` to both sides

`2(4)/(7)=b`

`y=-(2)/(7)x+2(4)/(7)`

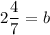
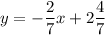
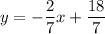`y=-(2)/(7)x+(18)/(7)` multiply both sides by 7

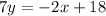`7y=-2x+18` subtract 7y from both sides

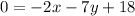`0=-2x-7y+18` change the signs

`2x+7y-18=0`

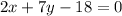
Answer:

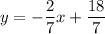`y=-(2)/(7)x+(18)/(7)` slope-intercept form

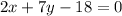`2x+7y-18=0` general form