Slope formula:
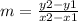 or
or
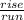
Coordinates given: (2, 6), (-2, 3)
Substitute for x and y in the formula: (2, 6) for (x1, y1) and (-2, 3) for (x2, y2)
slope of the line:
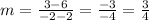
Your slope =
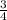
Another way to find the slope is by finding the
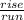
(Check the attached picture)
If you notice in the picture, the
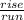 is equal to the slope we just found; however, this is a simpler way to find the slope.
is equal to the slope we just found; however, this is a simpler way to find the slope.
The rise is 3 and the run is 4, you use any two points on the line, let's take (2, 6), (-2, 3), for example. At (-2, 3), you rise 3 points until you reach horizontal line on the graph where the coordinates (2, 6) are plotted, then you run 4 points until you reach (2, 6).