Question

suppose that A and B are independent events. if P(A)=.4 and P(B)=.1, what is P(A∩B¹)? A .54 B .06 C .36 D .04

Answer 1

ANSWER


`P(A \cap B')=0.36`


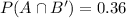
Step-by-step explanation

If event A and event B are independent, then


`P(A \cap B)= P(A ) * P(B)`

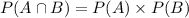
otherwise A and B are dependent events.



We were given that,


`P(A) = 0.4`


and


`P(B) = 0.1`


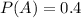
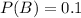
and we were asked to evaluate



`P(A \cap B')`

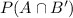
Since A and B are independent,


`P(A \cap B') = P(A ) * P(B')`
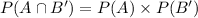
Recall that,




`P(B') = 1 - P( B)`


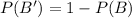
This implies that,


`P(A \cap B') = P(A ) * (1 - P(B) )`


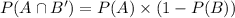
We now substitute the above values to obtain,



`P(A \cap B') = 0.4 * (1 - 0.1 )`







`P(A \cap B') = 0.4 * 0.9`



`P(A \cap B') = 0.36`


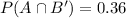
Therefore the correct answer is C.