Question

use the discrminant to determine all values of k which would result in the equation -3x^2-6x+k=0 having real,unequal roots.​ must be right ty helppp asap

Answer 1

`k>-3`

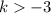
Explanation:

We have the equation:

`-3x^2-6x+k=0`

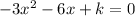
Where a = -3, b = -6, and c = k.

And we want to determine values of k such that the equation will have real, unequal roots.

In order for a quadratic equation to have real, unequal roots, the discriminant must be a real number greater than 0. Therefore:

`b^2-4ac>0`

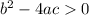
Substitute:

`(-6)^2-4(-3)(k)>0`

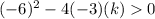
Simplify:

`36+12k>0`

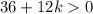
Solve for k:

`12k > -36`

`k>-3`

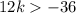
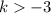
So, for all k greater than -3, our quadratic equation will have two real, unequal roots.

Notes:

If k is equal to -3, then we have two equal roots.

And if k is less than -3, then we have two complex roots.