Question

Based on the polynomial remainder theorem, what is the value of the function when x=−6 ?

f(x)=x4+8x3+10x2−7x+40

Answer 1

ANSWER


`f( - 6) = 10`


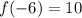
Step-by-step explanation

The given function is

`f(x) = {x}^(4) + 8 {x}^(3) + 10 {x}^(2) - 7x + 40`

According to the remainder theorem,


`f( - 6) = R`
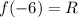
where R is the remainder when

`f(x)`

is divided by

`x + 6`


We therefore substitute the value of x and evaluate to obtain,


`f( - 6) = { (- 6)}^(4) + 8 {( - 6)}^(3) + 10 { (- 6)}^(2) - 7( - 6)+ 40`





`f( - 6) = 1296 + 8 ( - 216) + 10 (36) - 7( - 6)+ 40`





`f( - 6) = 1296 - 1728 + 360 + 42+ 40`



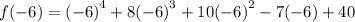
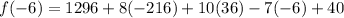
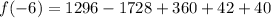
This will evaluate to,



`f( - 6) = 10`


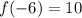
Hence the value of the function when

`x = - 6`

is

`10`



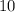
According to the remainder theorem,

`10`
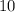
is the remainder when


`f(x) = {x}^(4) + 8 {x}^(3) + 10 {x}^(2) - 7x + 40`
is divided by

`x + 6`